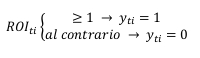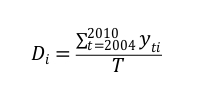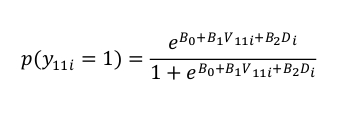di: Stefano De Santis, Stefania Cardinaleschi, Marina Schenkel, Francesco G. Truglia
EyesReg, Vol.6, N.4, Luglio 2016
L’indebolimento dell’identità locale e delle relazioni distrettuali è una delle conseguenze negative dell’aumento della concorrenza a livello globale. Secondo alcuni recenti studi (De Maria e Grandinetti, 2014; Di Giacinto et al, 2014; Becattini, 2015; Storai, 2016;), la delocalizzazione e l’internazionalizzazione costituirebbero una minaccia per l’ atmosfera industriale costruita nel lungo periodo di crescita.
Nella prospettiva indicata da queste ricerche, il presente lavoro esamina gli effetti spaziali sulla performance delle imprese a livello di comune, tenendo conto degli spillovers fra aree contigue.
Si ricorda che le analisi del caso italiano che prendono in considerazione la profittabilità delle imprese basandosi su dati individuali (Dosi, 2008; Secchi e Tamagni, 2009; Bottazzi et al. 2010, Dosi et al., 2011, Schenkel e Cassetta, 2014) trovano un legame positivo fra produttività e profitti, ma non fra queste variabili e la crescita dell’impresa. Per quanto riguarda le variabili “strategiche” fondamentali (investimenti, internazionalizzazione, integrazione verticale) i risultati cambiano a seconda delle variabili dipendenti e dei metodi di stima.
Dati
La ricerca si basa su una base dati creata ad hoc, con il matching dei dati di bilancio delle Camere di Commercio e quelli dell’Archivio Statistico delle Imprese Attive (ASIA). Le unità di analisi sono le imprese con obbligo di bilancio, in forma di panel non bilanciato. Il data set considerato include circa 700.000 società di capitale osservate per ogni anno nel periodo compreso tra il 2004 e il 2011. Queste imprese, pur rappresentando il 15,6% del totale, nell’anno 2012 costituiscono il segmento più importante dell’economia italiana in termini di fatturato (61,1%), valore aggiunto (55,3%), MOL (43,2%), occupazione (60,7%).
Metodologia e obiettivi
Per valutare congiuntamente la dipendenza contemporanea e ritardata, identificando gli spillover e gli spinoff che determinano la dinamica spazio-temporale, si è adottata la metodologia di analisi econometrica sviluppata da Anselin (2002). La variabile presa in esame è ROIti dove t =tempi (2004-2011) e i= comuni (base territoriale 2011). Stime effettuate su altre misure della profittabilità delle imprese, quali il MOL e il ROE, non hanno rilevato alcun effetto spaziale o temporale
L’elaborazione si articola in 5 passi.
- Si ricodifica il ROIti in forma binaria:
- Si ricodificano gli elementi wij della matrice di contiguità spaziale W:
- Si moltiplica la matrice W per il ROI ricodificato del 2011 (y11i), indicando con Ji l’insieme dei comuni contigui al comune i-esimo, e wij*y11ij la variabile indicatrice
La variabile vi è nota come Spatially legend , mentre Ls y=wijyij è il lag o ritardo spaziale.
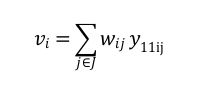
è il numero di comuni con valore ROI ricodificato y11ij =1 che compongono il vicinato dell’i-esimo comune. Mentre
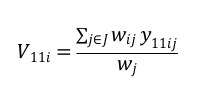
è la proporzione di comuni contigui al comune i-esimo che hanno un valore di ROI ricodificato pari a 1.
- Per gli anni 2004-2010 si calcola la proporzione delle volte che yti =1. In questo caso t = 2004, 2005,…,2010, mentre T=7 è il numero degli anni considerati.
- Si stima il modello logistico, che spiega la probabilità che il ROI ricodificato sia uguale a 1
La stima dei parametri del modello logistico
I risultati della stima del modello logistico sono presentati nella seguente tabella (Tab. 1).
Tabella 1 – Stima dei parametri del modello logistico
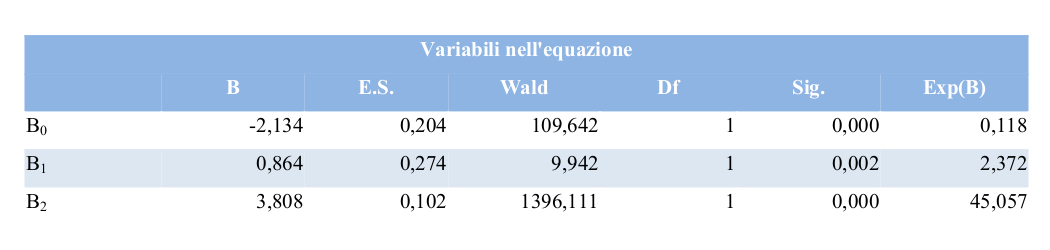
Exp(B0): registra come varia la probabilità di y11i=1 rispetto alla probabilità contraria y11i=0 (odds) per i comuni senza vicinato nei quali negli anni 2004-2010 il ROI < 0.
Exp(B1): misura gli effetti spaziali quindi l’interazione tra il comune i-esimo e i comuni ad esso contigui. Tali effetti sono noti in letteratura come spillover.
Exp(B2): registra la persistenza/volatilità temporale del comune i-esimo in relazione ai livelli di ROI registrati, sempre nello stesso comune, negli anni 2004-2010.
Si nota che gli effetti temporali Exp(B2), che misurano la persistenza nel tempo, sono maggiori degli effetti spaziali Exp(B1). Tuttavia anche gli effetti spaziali sono significativi, indicando quindi la presenza di spillover fra comuni contigui.
Il modello classifica correttamente circa l’ 83% dei comuni, tale percentuale arriva al 95% per i comuni con un ROI ≥ 0 (Tabella 2).
Inoltre, la capacità di discriminare correttamente è maggiore per i comuni con ROI ≥ 0, che sono il 76,9% del totale.
Tabella 2 – Classificazione dei comuni in base al modello logistico

Ulteriori risultati
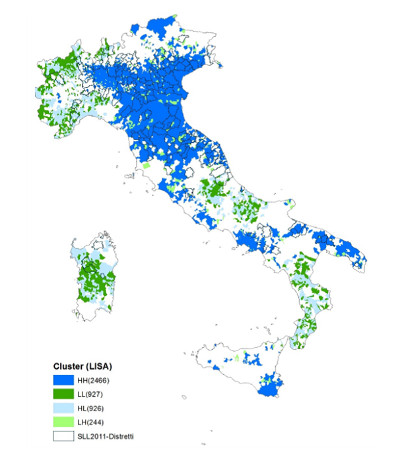
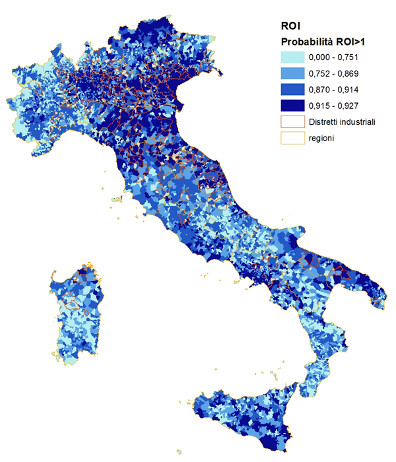
A partire dalle stime della stima delle probabilità che il ROI sia maggiore di 1 (v. figura 2 in appendice) si sono individuati dei cluster di comuni contigui con livelli simili di probabilità. A tale scopo si è utilizzato l’indice di autocorrelazione di Moran sia nella versione globale ( I ) che locale (LISA).
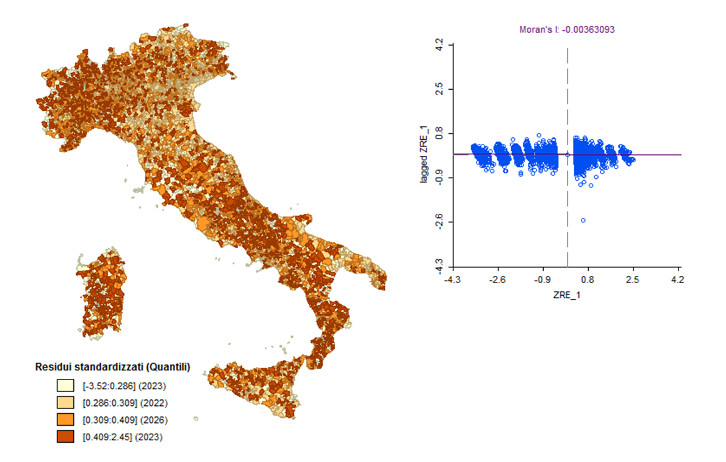
L’indice I è pari a 0,43 è segnala la presenza di un processo aggregativo di intensità media, ma significativa (p<0,001)
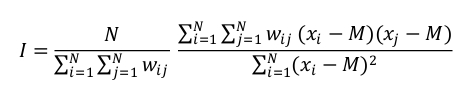
La versione locale dell’indice di Moran (Local Indicators of Spatial Association – LISA)
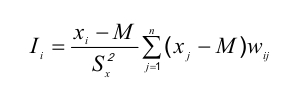
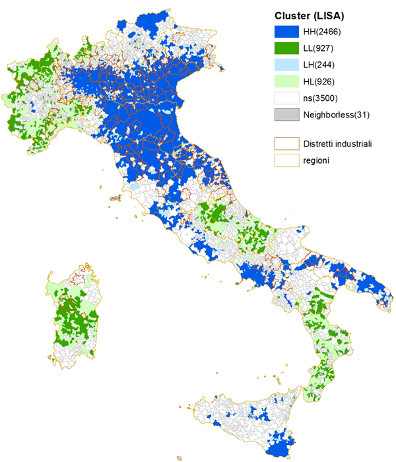
consente di individuare i comuni che forniscono un contributo significativo all’autocorrelazione globale indentificando 5 tipi di clusters.
- Comuni contigui con alti valori di prob(ROI>1);
- Comuni contigui con valori bassi di prob(ROI>1);
- Comuni con valori alti contigui a comuni con valori bassi di prob(ROI>1);
- Comuni con valori bassi contigui a comuni con valori alti di prob(ROI>1);
Ns. Comuni che non apportano un contributo significativo.
Figura 1 – Aggregazione dei comuni in relazione ai valori di autocorrelazione locale
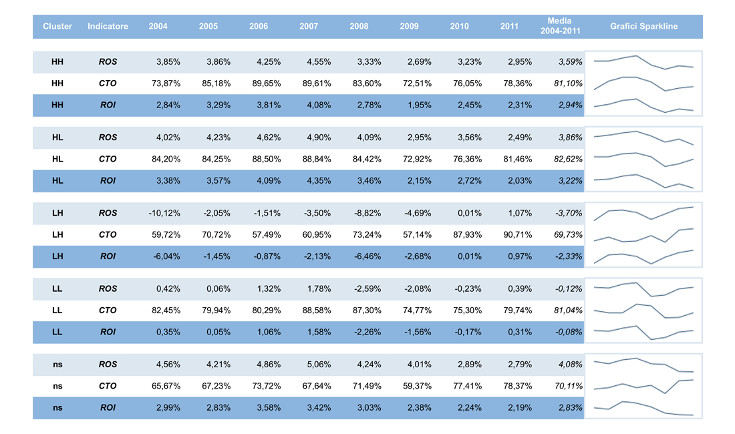
La seguente tabella (tab. 4) presenta per ogni cluster l’andamento del ROI e delle sue componenti ROE (Return on Equity) e CTO (Capital Turn Over). Si può notare come l’andamento nel periodo 2004-2011 diverga non solo fra le diverse tipologie di cluster, ma anche fra le misure di profittabilità indicate all’interno delle singole tipologie. Questo risultato suggerisce di approfondire l’analisi di diverse misure della profittabilità delle imprese, e delle loro reciproche interrelazioni.
Tabella 3 – Andamento della redditività industriale, mark-up e fatturato nei cluster
Infine le seguenti tabella (Tab. 4) e figura (Fig. 4) confrontano i cluster identificati nell’analisi con la configurazione in distretti. Si può notare che c’è una buona coincidenza fra le due classificazioni, dato che il modello classifica “correttamente” una grande percentuale di comuni (circa l’ 83% dei casi). Inoltre, la capacità di discriminare correttamente è maggiore per i comuni “ di successo”, cioè con ROI ≥ 0 , ai quali appartiene più della metà dei comuni distrettuali.
Questo duplice risultato si può interpretare come una buona notizia per il sistema distrettuale: l’”atmosfera industriale” non solo non si è dissolta, ma risulta ancora benefica per la salute delle imprese inserite in un distretto.
Tabella 4 – Cluster e distretti: confronto fra le due tassonomie
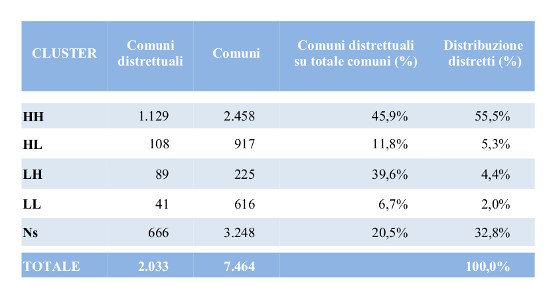
Figura 2 – Rappresentazione grafica delle tassonomie dei cluster e dei distretti
Conclusioni
Il principale esito dell’analisi effettuata è la prevalenza degli effetti temporali su quelli spaziali. Anche questi ultimi tuttavia sono significativi, per cui non è confermata l’ ipotesi della sparizione dell’effetto territorio. I cluster identificati nell’analisi riproducono largamente la struttura distrettuale, soprattutto per i comuni in cui le imprese hanno una migliore performance. Inoltre i comuni distrettuali appartengono in gran parte ai cluster di maggior successo. Non sembra quindi che la frammentazione delle filiere produttive e la diffusione delle reti internazionali di imprese abbiano intaccato il lascito della formazione e del consolidamento dei distretti, almeno per quanto riguarda la profittabilità delle imprese localizzate in uno di essi, appartengano o no all’industria caratteristica del distretto stesso. In futuro si cercherà di migliorare la misura della performance delle imprese. Rimarrà poi da approfondire l’effetto di tale variabile sui livelli di reddito complessivi, collegando questi ultimi, in un’ottica di lungo periodo, ad altre variabili di ordine geografico e istituzionale.
Stefano De Santis, ISTAT
Stefania Cardinaleschi, ISTAT
Marina Schenkel, Università di Udine
Francesco G. Truglia, ISTAT
Bibliografia
Anselin L. (2002), Under the Hood. Issues in the Specification and Interpretation of Spatial Regression Models, Regional Economics Application Laboratory (REAL), University of Illinois.
Beccattini G. (2015), La coscienza dei luoghi, Roma: Donzelli.
Bottazzi G., Dosi G., Jacoby N., Secchi A., Tamagni F. (2010), Corporate performances and market selection: some comparative evidence, Industrial and Corporate Change, 19: 1953-1996
De Marchi V., Grandinetti. R. (2014), Industrial Districts and the Collapse of The Marshallian Model: Looking at the Italian Experience, Competition and Change, 18: 70–87.
Di Giacinto V., Gomellini M., Micucci G., Pagnin M. (2014), Mapping local productivity advantages in Italy: industrial districts, cities or both?, Journal of Economic Geography 14: 365–394.
Dosi G. (2008), Regolarità statistiche nell’evoluzione dei settori industriali: l’evidenza empirica e le sfide per la teoria, l’Industria. Rivista di Economia e Politica Industriale, XXIX: 185-219.
Dosi G., Grazzi M., Tomasi C., Zeli A. (2011) , L’industria manifatturiera negli ultimi due decenni prima della crisi: le micro-dinamiche sottostanti ai trend aggregate, Economia e Politica Industriale, 38: 63-95.
Schenkel M., Cassetta E. (2014), La performance delle piccole e medie imprese italiane: un’analisi empirica, Rivista di Statistica Ufficiale: 221-241.
Secchi A., Tamagni F. (2009), Un’analisi empirica delle relazioni tra crescita d’impresa, produttività e profittabilità, in Rondi L., Silva F. (a cura di) Produttività e cambiamento nell’industria italiana. Indagini quantitative, Bologna: Il Mulino: 39-65.
Storai D. (2016), Le trasformazioni dei distretti industriali italiani, mimeo.
Appendice